引用元:https://www.ioccc.org/2006/stewart/stewart.c
審査員・作者による説明:https://www.ioccc.org/2006/stewart/hint.text
動作
フラクタルの一種である反復関数系の描画を行う。
シェルピンスキーのギャスケット。
$ gcc -o stewart stewart.c
$ ./stewart 400 1000000 gasket > gasket.xbm
$ convert gasket.xbm gasket.png
 図:gasket.xbm(シェルピンスキーのギャスケット)
図:gasket.xbm(シェルピンスキーのギャスケット)
ドラゴン曲線。
$ ./stewart 400 1000000 dragon > dragon.xbm
$ convert dragon.xbm dragon.png
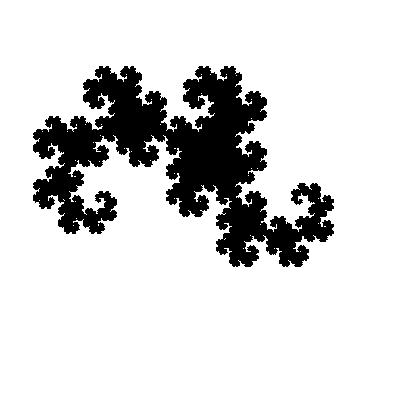 図:dragon.xbm(ドラゴン曲線)
図:dragon.xbm(ドラゴン曲線)
リアルなシダ。
$ ./stewart 400 1000000 fern > fern.xbm
$ convert fern.xbm fern.png
 図:fern.xbm(シダ画像)
図:fern.xbm(シダ画像)
リアルな木。
$ ./stewart 400 1000000 tree2 > tree2.xbm
$ convert tree2.xbm tree2.png
 図:tree2.xbm(木)
図:tree2.xbm(木)
IOCCCのロゴを目指したもの。
$ ./stewart 400 1000000 ioccc > ioccc.xbm
$ convert ioccc.xbm ioccc.png
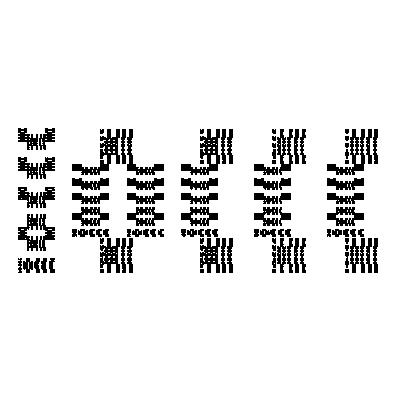 図:ioccc.xbm(IOCCCのロゴになりたかったもの)
図:ioccc.xbm(IOCCCのロゴになりたかったもの)
他にも多数の設定が添付されている。
解説
[[1992/imc]]や[[1994/tvr]]など、フラクタルを生成する作品はいくつも実績があるけれど、反復関数系(IFS)を扱うものは初とのこと。
設定ファイルのフォーマットは次の通り。
<num ifs> <x min> <y min> <x max> <y max>
<a> <b> <c> <d> <e> <f> <p>
<a> <b> <c> <d> <e> <f> <p>
<a> <b> <c> <d> <e> <f> <p>
.
.
.
aからfは、(prevx, prevy)から(x, y)に点を移すときの式の座標。
x = a * prevx + b * prevy + e;
y = c * prevx + d * prevy + f;
最後のpは、その式が実行される確率とのこと。
画像出力はXBMという古いフォーマット。
コードは、変数宣言がvoid*の1つだけで、long型の値もdouble型の値もポインタもすべてこれにキャストして扱うようになっている。
実質的に、型がない状態。
プリプロセスをするとキャストがたくさん出てくるので、みるのが大変。
賞名は[[2006/monge]]と対称的になっている。